重拾数学1－箱线图

来到新公司实习之后，发现我将要做的工作是我一直以来期待的关于机器学习和人工智能的东西， 兴奋至于也终于意识到不得不好好补补自己的数学了，于是打算写一个重拾数学的学习笔记， 尽量做到每天一篇，看看能坚持多久吧。

首先是在KHanACADEMY上遇到的第一个问题，就是box plot,

The box plot (a.k.a. box and whisker diagram) is a standardized way of displaying the distribution of data based on the five number summary: minimum, first quartile, median, third quartile, and maximum.

Box plot中文应该是叫箱线图，主要用来以较少的数据直观的描述数据集的分布情况，其主要用的值有最小值、 中位数、最大值、第一四分位数和第三四分位数等。

举例：
请给出一下有序数列的box plot图，4，5，7，7，7，8，10，11，11，13，13，14.

解：
首先需要找到的五个点以及其对应的寻找方法如下：

1. 最大值：数列中的最大值
2. 最小值：数列中的最小值
3. 中位数：如果数列中数的个数为奇数，则直接取数列长度除以2向上取整的位置所在的数 （如10，20，30，40，50中，数列长度为5，5/2向上取整为3，所以，中位数为位于第三个位置的数30）； 如果数列中数的个数为偶数，则取数列长度除以2的位置的数，以及其后面的数，在本例中，即第六和第七位数， 分别为8和10，然后在求二者的平均数，本例中即为9，所以本例中的数列的中位数即为9.
4. 第一四分位数：如果数列中数的个数为奇数，则第一四分位数为去掉中位数之后前面剩余的数所组成的数列的中位数， 如果数列中数的个数为偶数，则第一四分位数为前面一半的数所组成的数列的中位数。
5. 第三四分位数：如果数列中数的个数为奇数，则第三四分位数为去掉中位数之后后面剩余的数所组成的数列的中位数， 如果数列中数的个数为偶数，则第三四分位数为后面一半的数所组成的数列的中位数。

找到以上所需的五个数之后，接下来就是要在数轴上画图的过程了，每个点具体的画法如下所示：

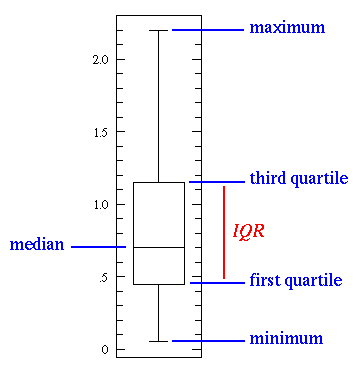
其中的第一四分位数到第三四分位数之间的长方形叫做interquartile range（IQR），IQR内部的线为中位数， IQR外面一上一下两条短线表示最大与最小值。

本例中最终的作图结果如下图：

参考：
1.Box Plot: Display of Distribution
2.Box plot - Wikipedia, the free encyclopedia
3.BOX PLOT–描述统计的一个简便工具